Ciência Florestal, Vol. 15, No. 3, 2005, pp. 293-305

FORMA DE TRONCO E SORTIMENTOS DE MADEIRA DE Eucalyptus grandis Hill ex Maiden, NA REGIÃO SUDESTE DO ESTADO DO RIO GRANDE DO SUL

TAPER AND ASSORTMENT OF WOOD FOR Eucalyptus grandis Hill ex Maiden,IN THESOUTHEAST REGION OF RIO GRANDE DO SUL

Ivanor Müller¹,César Augusto Guimarães Finger² , Paulo Renato Schneider³

^1. Engenheiro Florestal, Dr., Professor Adjunto do Departamento de Estatística, Centro de Ciências Naturais e Exatas,
Universidade Federal de Santa Maria, CEP: 97.105-900, Santa Maria (RS). ivanormuller@smail.ufsm.br.
^2. Engenheiro Florestal, Dr. Professor Adjunto do Departamento de Ciências Florestais, Centro de Ciências Rurais,
Universidade Federal de Santa Maria, CEP: 97.105-900, Santa Maria (RS). finger@smail.ufsm.br.
^3. Engenheiro Florestal, Dr. Professor Titular do Departamento de Ciências Florestais, Centro de Ciências Rurais,
Universidade Federal de Santa Maria, CEP: 97.105-900, Santa Maria (RS). paulors@smail.ufsm.br.

Code Number: cf05029

RESUMO

No presente trabalho, foi estudada a forma de tronco do Eucalyptus grandis Hill ex Maiden, com base em 261 árvores cubadas, cobrindo diâmetros entre 8,0 cm e 74,0 cm ao nível do dap (diâmetro à altura do peito) originadas de florestas de propriedade da Aracruz Celulose S. A., localizadas em hortos florestais da Depressão Central e do Escudo Sul-Riograndense, no Rio Grande do Sul, para a determinação de volume e formação de sortimentos de madeira em duas classes: serraria, compreendendo toras com diâmetro na ponta fina superior a 25,0 cm com casca e com comprimentos de 5,60 metros, 4,20 metros e 2,80 metros, priorizando a formação de sortimentos com o maior comprimento; indústria, para troncos ou porções destes com diâmetros entre 8,0 cm e 25,0 cm com casca. O polinômio do quinto grau, tendo como variável dependente os diâmetros relativos (d_i/d) e independente as alturas relativas (h_i/h), foi selecionado para descrever a forma, com estratificação dos dados em três classes de diâmetro à altura do peito: diâmetro  até 20,0 cm; entre 20,0 cm e 30,0 cm e maiores que 30,0 cm, com coeficientes de determinação superiores a 0,97 e erro padrão da estimativa inferior a 6,2 %, permitindo estimar o volume absoluto e relativo dos sortimentos por integração da função de forma. O ajuste do modelo para o conjunto de árvores cobrindo toda a amplitude de diâmetros gerou um coeficiente de determinação igual à 0,98 e erro padrão da estimativa igual a 6,54 % permitindo também selecionar o modelo para ajuste da forma e obtenção dos sortimentos.

Palavras-chave: Forma de tronco; sortimento; volume; Eucalyptus grandis.

ABSTRACT

This  study  had  the  objective of studing the stem shape of  Eucalyptus  grandis Hill  ex  Maiden, based  on  261 trees, with diameters at breast height (DBH) ranging from 8 cm to 74 cm, originated from Aracruz Celulose S. A. forests, located at Depressão Central and Escudo Sul-Riograndense, in Rio Grande do Sul state, to determine the volume and assortment of wood in  two  classes: timber (logs with 25 cm of minimum diameter, with bark, and lengths of 5,6;  4,2 and 2,8 m, prioritizing the higher length assortments formation) and industry (stems or portions of stem with diameters between 8 and 25 cm with bark). The fiftieth degree polynomial, having as dependent  variable the relative diameters (d_i/d) and independent variable the relative heights (h_i/h) was selected to describe the shape, with data stratification in three diameter classes (DBH): diameter until 20 cm; between 20 and 30 cm and larger than 30 cm, with coefficient of determination higher than 0,97 and standard error of the estimation lower than 6,2 %, allowing to estimate the relative and absolute volume of the assortments through integration of form function. The model adjustment for the trees complex covering all the diameters breadth generated a coefficient of determination equal to 0,98 and a standard error of the estimation equal to 6,54%, also allowing to select the model to describe the shape and assortment prediction.

Key words: Stem shape; assortment; volume; Eucalyptus grandis

.INTRODUÇÃO

O gênero Eucalyptus é largamente empregado no florestamento e reflorestamento em todas as regiões do Rio Grande do Sul. Esse gênero é importante pois, além do aproveitamento da madeira como fonte energética, é usado para a fabricação de celulose, chapas, construção civil e outros.

Uma das grandes dificuldades do manejo florestal e, em especial da avaliação econômica de povoamentos florestais desta espécie, reside na inexistência de tabelas de sortimento apropriadas que possibilitem determinações rápidas do estoque de madeira para diferentes tipos de aproveitamento. Em razão disso, muitas pesquisas têm sido realizadas com o objetivo de descrever, de forma otimizada, a classificação dos fustes segundo sua qualidade, dimensões e possibilidades de utilização, garantindo além da classificação física, uma melhor remuneração da madeira, com a destinação de toras de diversas bitolas ao mercado específico. Além disso, permite ao administrador florestal prognosticar em diversos horizontes, os sortimentos de madeira, para diferentes classes de sítio, permitindo planejar a produção física de toras, bem como a sua renda.

O presente trabalho foi desenvolvido com o objetivo de determinar o volume absoluto e relativo dos sortimentos de madeira para aproveitamento de toras em serraria, partindo de bitolas previamente definidas em relação a um diâmetro mínimo na ponta fina e de comprimentos pré-estabelecidos de acordo com as exigências atuais do mercado.

REVISÃO BIBLIOGRÁFICA

Independente das irregularidades das secções transversais dos troncos, as árvores possuem determinado tipo de forma de tronco que varia com a espécie e em função de vários fatores como o sítio, a densidade do povoamento, a intensidade do vento que age sobre a copa das árvores, e as intervenções silviculturais aplicadas nos povoamentos, como os desbastes e a desrama (Schneider, 1993).

Segundo o autor, um grande número de estudos sobre a forma de troncos foram desenvolvidos para demonstrar como obter diâmetros e respectivos volumes com base em alturas relativas tomadas ao longo do fuste.

Prodan (1965) desenvolveu pesquisas nesse sentido e concluiu que o tronco das árvores deveria ser dividido em, pelo menos, três secções distintas para efetuar o estudo de forma. Posteriormente, Jokela (1974) demonstrou que a forma de tronco de Picea excelsa é constituído de três partes distintas, sendo a parte côncava inferior descrita por uma hipérbole, a parte central do fuste por uma função logarítmica e a parte superior por um cone.

Segundo Spurr (1952), foi Schuberg que, em 1881, introduziu o conceito de quociente de forma como a relação entre dois diâmetros tomados, respectivamente, a metade da altura da árvore e, a 1,30 metros do solo, desenvolvendo-se, partindo daí, uma série de pesquisas sobre forma de tronco para definição de sortimentos de madeira.

Hozak et al. (1969), para o estudo de forma de tronco de Pinus, no Canadá, utilizaram uma função expressa por uma parábola, tendo como variáveis dependentes e independentes os diâmetros e alturas relativas respectivamente.

Schneider (1984) selecionou entre vários modelos de forma de tronco um polinômio do quinto grau, tendo como variáveis dependentes e independentes os diâmetros e alturas relativas, respectivamente, para estimar o volume dos sortimentos das árvores de Pinus elliottii na região do Planalto Médio do Rio Grande do Sul.

MATERIAL E MÉTODOS

A espécie estudada, no presente trabalho, foi o Eucalyptus grandis Hill ex Maiden, sendo  os dados coletados em povoamentos florestais de propriedade da Empresa Aracruz Celulose S. A., com sede no município de Guaíba, a 30 km de Porto Alegre, no estado do Rio Grande do Sul, em talhões do Horto Florestal Passo da Estância, do Horto Florestal Barba Negra e do Horto Florestal Calderon. A área de estudo localiza-se a 30⁰ 20^´ de latitude sul e 51⁰ 26^´ de longitude oeste do Meridiano de Greenwich. A altitude dessa região se situa em torno de 100 metros.

O tipo de clima da região é o “Cfa”, mesotérmico subtropical, com verões quentes e sem estação seca, segundo a classificação climática de Köeppen (Moreno, 1961). A temperatura média anual é de 16 ⁰C, sendo que a temperatura média do mês mais frio é de 9,2 ⁰C e a do mês mais quente não ultrapassa 24,6 ⁰C. A precipitação anual média é de 1.500 mm, com máxima precipitação nos meses de julho, agosto e setembro.

O solo da área é classificado como sendo da unidade de mapeamento Pinheiro Machado. Esses são solos litólicos eutróficos, de textura média, relevo fortemente ondulado e substrato de granito com afloramento de rochas. São solos pouco desenvolvidos, com argila de atividade alta e não-hidromórficos (Lemos et al., 1973).

Os povoamentos florestais foram implantados em espaçamento de 3 x 2 metros, perfazendo 1.666 árvores por hectare no momento do plantio. Esses povoamentos foram desbastados ao longo do tempo com o objetivo inicial de formar uma área de produção de sementes, remanescendo aos 15 anos, aproximadamente, duzentas árvores por hectare.

Para o estudo da forma de tronco e obtenção dos sortimentos, foram abatidas 261 árvores, cobrindo uma amplitude diamétrica de 8,0 a 74,0 cm de dap, distribuídas proporcionalmente em classes de 10 cm de diâmetro, o que garantiu uma representatividade de cerca de 29 em cada classe diamétrica. A cubagem das árvores foi realizada pelo método de Smalian, com secções nas posições de 0,10 m; 0,30 m; 1,30 m e, partindo desse ponto, de 1,0 em 1,0 metro, até o ápice das árvores.

As árvores cubadas originaram 8.146 pares de dados das variáveis dependentes e independentes, definidas pelos diâmetros relativos e alturas relativas das equações de forma de tronco testadas.

Num primeiro momento, foram analisadas as árvores-amostra de uma forma conjunta e, posteriormente, por classes diamétricas, partindo da distribuição das árvores-amostra em três classes de diâmetro, respectivamente, menor que 20,0 cm, de 20,0 cm a 30,0 cm e acima de 30,0 cm, permitindo assim avaliar o ajuste e a precisão das equações de forma.

Para o ajuste da forma de tronco das árvores bem como para a determinação dos sortimentos, foram testadas as equações de forma de tronco discriminadas na Tabela 1.

As funções de forma de tronco foram processadas no pacote estatístico SAS, para computador IBM da Universidade Federal de Santa Maria.

As alturas (h_i) foram também estimadas por uma equação polinomial do quinto grau, porém, tendo como variáveis dependentes as alturas relativas (h_i/h) e, como independentes os diâmetros relativos (d_i/d). Nesse caso, foi considerado o diâmetro mínimo, na ponta mais fina da tora, de 8,0 cm com casca, para quantificar o volume total aproveitável da árvore, e de 25,0 cm com casca, para o volume de toras para serraria.

O modelo ajustado foi o polinômio de quinto grau:

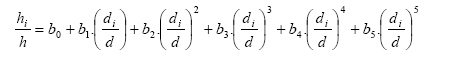
Em que: h_i = Altura  até um  diâmetro  limite  determinado,  em metros; h = Altura total da árvore, em metros; d_i = Diâmetro limite dado para a ponta mais fina da tora, em centímetros; d = Diâmetro à altura do peito, em centímetros.

O fuste aproveitável foi otimizado para formar, preferencialmente, toras com o maior comprimento, e o restante do fuste, classificado nas classes ligeiramente inferiores, de menor comprimento.

A parte do fuste com diâmetro superior a 8,0 cm e inferior a 25,0 cm com casca, juntamente com toda a parte do fuste que não possibilitou a formação de uma tora com os comprimentos definidos, foi considerada como volume para celulose e energia.

Os sortimentos de madeira para serraria foram determinados por meio de um programa computacional em Linguagem Basic, elaborado especificamente para a solução do problema, sendo classificados e expressos em volume, em m³, e em número de peças correspondentes segundo os seguintes critérios:

a) S1 = Madeira para serraria com diâmetro na ponta fina da tora superior a 25,0 cm com casca e comprimento de 5,60 metros;

b) S2 = Madeira para serraria com diâmetro na ponta fina da tora superior a 25,0 cm com casca e comprimento de 4,20 metros;

c) S3 = Madeira para serraria com diâmetro na ponta fina da tora superior a 25,0 cm com casca e comprimento de 2,80 metros.

Os volumes dos sortimentos foram determinados por integração da função de forma, expressa por um polinômio do quinto grau, da seguinte maneira:

a)      Volume até a altura na qual o diâmetro corresponde a 8,0 cm com casca:

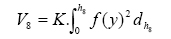
b)      Volume até a altura na qual o diâmetro corresponde a 25,0 cm com casca:

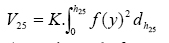
c)      Volume do fuste até a altura com diâmetro entre 8,0 e 25,0 cm com casca:

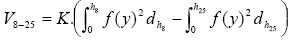
Em que: h₈ = Comprimento do fuste, em metros, até o diâmetro de 8,0 cm com casca; h₂₅ = Comprimento do fuste, em metros, até o diâmetro de 25,0 cm com casca; f(y) = Função de forma do tronco; K = (π/4)/10.000 = Constante.

RESULTADOS E DISCUSSÕES

O ajuste dos modelos apresentados na Tabela 1, para o conjunto de dados amostrados, está resumido na Tabela 2, na qual são apresentados os coeficientes e os parâmetros estatísticos utilizados na escolha da melhor equação da forma de tronco para o conjunto das árvores-amostra.

TABELA 2: Coeficientes  e  parâmetros  estatísticos  das   equações   testadas  para  o  conjunto  das  árvores-amostra.

TABLE 2: Coefficients and statistical parameters of the equations tested for the whole tree-sample.

Eq.	Coeficientes						Estatísticas
	b0	b1	b2	b3	b4	b5	R2aj	Sxy%
1	1,084775	-0,911593					0,9467	9,73673
2	1,184862	-2,046045	0,922054				0,9175	20,66835
3		2,641991	-3,160614				0,4346	92,62701
4	1,183162	-2,053553	0,984735				0,9167	20,76124
5	1,250916	0,801078					0,1612	-204,50083
6	0,494251	1,217251	0,001783ns	0			0,5537	28,17430
7	0,227301	1,367607					0,6996	23,11396
9	0,037990	0,712890	0,002500				0,9961	-13,91306
10	0,811095	4,506802					0,2676	-191,08437
11	-10,262867	40,387899	-50,208815	21,268658			0,9744	6,74160
12	-8,304026	29,349469	-27,290651	0,487636ns	6,946965		0,9745	6,73328
13	-98,747659	669,823163	-1816,332277	2464,710632	-1667,160079	448,932706	0,9790	6,11625
14	0,826875	-1,122854					0,7094	38,78200
15	1,185069	-2,130717	0,999385				0,9186	20,52143
16	1,129151	-1,772493	2,451167	-1,820016			0,9690	7,42584
17	1,154108	-2,429508	5,624098	-6,902098	2,575791		0,9716	7,10972
18	1,185900	-3,810050	16,215233	-36,237954	36,157220	-13,518423	0,9760	6,53843

Em que: Eq. = equações; ns = não-significativo ao nível de significância de 5% (p > 0.05); b₀, b₁, b₂, b₃, b₄ e b₅ = coeficientes; R²_aj = coeficiente de determinação ajustado; S_xy% = erro padrão em percentagem.

Nas Tabelas 3, 4 e 5, são apresentados os coeficientes e os parâmetros estatísticos utilizados na escolha da melhor equação da forma de tronco para a classe diamétrica inferior a 20,0 cm, para a classe entre 20,0 cm e 30,0 cm e para a classe superior a 30,0 cm de diâmetro respectivamente.

TABELA 3: Coeficientes  e  parâmetros  estatísticos das equações testadas para os dados da classe inferior a 20,0 cm.

TABLE 3: Coefficients and statistical parameters of the equations tested for the data of the lower than 20 cm class.

Eq.	Coeficientes						Estatísticas
	b0	b1	b2	b3	b4	b5	R2aj	Sxy%
1	1,112464	-0,909174					0,9458	9,03585
2	1,241156	-2,078322	0,914950				0,9215	18,51857
3		2,797322	-3,355094				0,4340	90,16342
4	1,241024	-2,101092	1,005015				0,9214	18,52797
5	1,302059	0,878632					0,1601	-229,83034
6	0,523077	1,112310	0,003219ns	0			0,5779	25,22119
7	0,248878	1,313350					0,7066	21,02868
8	0,052442	0,658818					0,9982	-10,53126
9	0,045054	0,646013	-0,000857				0,9982	-10.50250
10	0,915316	4,893658					0,2745	-213,61525
11	-10,455017	41,151146	-51,063446	21,572244			0,9747	6,18084
12	-11,305599	45,951164	-61,040194	30,625844	-3,028175ns		0,9746	6,18105
13	-119,088501	810,432063	-2199,080346	2978,276408	-2006,933468	537,639936	0,9813	5,30369
14	0,881380	-1,193447					0,6998	36,20672
15	1,241349	-2,184447	1,011824				0,9218	18,48395
16	1,154888	-1,796261	2,542742	-1,897217			0,9713	6,57847
17	1,171585	-2,258019	4,803739	-5,538466	1,843639		0,9726	6.42128
18	1,206494	-3,871947	17,474848	-41,220006	43,214283	-16,804053	0,9789	5,63359

Em que: Eq. = equações; ns = não-significativo ao nível de significância de 5% (p > 0.05); b₀, b₁, b₂, b₃, b₄ e b₅ = coeficientes; R²_aj = coeficiente de determinação ajustado; S_xy% = erro padrão em percentagem.

TABELA 4: Coeficientes e parâmetros estatísticos das equações testadas para os dados da classe de 20 cm a 30 cm.

TABLE 4: Coefficients and statistical parameters of the equations tested for the data of the class of 20 to 30 cm.

Equação	Coeficientes						Estatísticas
	b0	b1	b2	b3	b4	b5	R2aj	Sxy%
1	1,083902	-0,901344					0,9534	8,97477
2	1,186453	-2,044425	0,923753				0,9240	19,73668
3		2,651527	-3,172891				0,4360	92,35821
4	1,186356	-2,063785	1,001763				0,9240	19,74203
5	1,292692	0,823262					0,1616	-206,43512
6	0,495287	1,026233	0,007480	0			0,5597	27,58588
7	0,226086	1,364726					0,7034	22,63978
8	0,024512	0,674683					0,9980	-9,99374
9	0,028702	0,681202	0,000436				0,9980	-9,98455
10	0,799939	4,437557					0,2601	-193,93951
11	-10,188021	40,185616	-50,041198	21,229896			0,9799	5,88744
12	-9,407704	35,790219	-40,918623	12,960531	2,763653ns		0,9800	5,88647
13	-101,974431	691,327252	-1872,169634	2535,544543	-1711,152184	459,650306	0,9848	5,13223
14	0,829052	-1,121145					0,7146	38,24547
15	1,186565	-2,131139	1,003789				0,9242	19,71584
16	1,131739	-1,802944	2,541831	-1,876058			0,9752	6,54060
17	1,153987	-2,389454	5,371054	-6,402035	2,292189		0,9774	6,25482
18	1,187034	-3,829835	16,417272	-36,966105	37,234274	-14,047486	0,9822	5,54096

Em que: ns = não-significativo  ao  nível  de  significância  de  5% (p  >  0.05);  b₀,  b₁, b₂, b₃, b₄ e b₅ = Coeficientes; R²_aj = coeficiente de determinação ajustado; S_xy% = erro padrão em percentagem.

TABELA 5: Coeficientes  e  parâmetros  estatísticos das equações testadas para o conjunto de dados da classe superior a 30 cm.

TABLE 5: Coefficients and statistical parameters of the equations tested for the dataset of the larger than 30 cm class.

Equação	Coeficientes						Estatísticas
	b0	b1	b2	b3	b4	b5	R2aj	Sxy%
1	1,051797	-0,934109					0,9602	9,33784
2	1,108171	-1,989324	0,913181				0,9225	21,86811
3		2,428460	-2,898915				0,4337	95,67873
4	1,107665	-1,999530	0,963744				0,9222	21,90018
5	1,348867	0,769089					0,1815	-171,62996
6	0,465797	1,396934	-0,000343ns	0			0,4936	33,30728
7	0,208601	1,452705					0,6643	27,11998
8	-0,048777	0,708933					0,9935	-15,32805
9	0,034924	0,829301	0,008116				0,9955	-12,67994
10	0,723192	4,294867					0,2873	-160,14625
11	-9,839628	38,404172	-47,466492	20,051363			0,9818	6,31010
12	-1,004481*	-11,377790	55,895184	-73,691153	31,349863		0,9830	6,09682
13	-71,123162	484,020742	-1325,096117	1825,115519	-1256,664666	344,949358	0,9854	5,65190
14	0,754567	-1,041430					0,7199	41,56979
15	1,108242	-2,047972	0,967573				0,9228	21,81816
16	1,086272	-1,618336	1,990402	-1,493173			0,9736	7,60732
17	1,126105	-2,608965	6,737493	-9,109467	3,883863		0,9787	6,82540
18	1,157379	-3,865643	16,216736	-35,190888	33,677488	-12,008856	0,9820	6,27293

Em que: ns = não-significativo  ao  nível  de  significância  de  5%  (p  >  0.05);  b₀,  b₁, b₂, b₃, b₄ e b₅ = coeficientes; R²_aj = coeficiente de determinação ajustado; S_xy% = erro padrão em percentagem.

Nas tabelas anteriores, observa-se que a maioria das equações testadas apresenta uma boa precisão estatística cujo coeficiente de determinação ajustado é superior a 0,9167 e o erro padrão da estimativa é inferior a 0,10834. Isso indica que tais equações poderiam ser utilizadas para estimar o volume dos sortimentos da espécie estudada.

No entanto, considerando a precisão estatística, a equação de número 18, expressa por um polinômio do quinto grau, tanto no conjunto total das árvores quanto nas classes diamétricas, foi a que apresentou um alto valor do coeficiente de determinação ajustado, variando entre 0,9760 e 0,9822, e um baixo valor do erro padrão da estimativa, o qual variou entre 0,03647 e 0,04293, o que corresponde a uma variação de 5,54096% e 6,53843% respectivamente. Esse modelo também permitiu estimar o volume dos sortimentos com um menor valor residual, determinado pela diferença absoluta entre o volume real e o volume estimado pela função. Por isso, foi o modelo selecionado para determinar o número de toras e o volume relativo dos sortimentos das árvores de Eucalyptus grandis Hill ex Maiden.

A determinação da altura correspondente ao diâmetro limite foi baseada nas variáveis dendrométricas d_i (diâmetro na posição i), h_i (altura na posição i), d (diâmetro à altura do peito) e h (altura total da árvore).

Na Tabela 6, encontram-se os coeficientes e as estatísticas de ajuste e precisão, calculados para os dados em conjunto único e para os dados agrupados em classes diamétricas para o polinômio do quinto grau tendo como variáveis independentes a relação d_i/d.

TABELA 6: Coeficientes e estatísticas de ajuste e precisão para o polinômio de quinto grau.

TABLE 6: Coefficients and adjustment statistics and precision of the fifth degree polynomial.

Classe	Coeficientes						R2aj.	Sxy%
(dap)	b0	b1	b2	b3	b4	b5
Total	0.99329904	-0.58025042	0.92061877	-3.47566288	2.69361491	-0.49533858	0.9801	8.87070
< 20 cm	0.99911124	-0.54135518	0.97021967	-3.55130390	2.69328718	-0.49075156	0.9828	8.54198
20 cm - 30 cm	1.00268450	-1.01979351	3.66765249	-9.37385623	7.87036252	-2.08827333	0.9871	7.12377
> 30 cm	1.00937080	-1.23615954	3.90818737	-9.47853614	7.95783748	-2.12652227	0.9869	6.98461

Em que:  dap =  diâmetro   à   altura   do   peito   (1,30 m),  em  centímetro;  b₀,  b₁,  b₂,  b₃,  b₄  e  b₅  =  coeficientes; R²_aj = coeficiente de determinação ajustado; S_xy% = erro padrão em percentagem.

Tendo em vista o alto grau de ajuste (> 98 %) e o baixo erro percentual (< 9 %), optou-se por utilizar o modelo para a determinação do comprimento das toras, porém de uma maneira mais individualizada, ou melhor, por classe diamétrica, sendo cada uma com seus respectivos coeficientes, e não de uma maneira única para todo o conjunto de árvores.

A Tabela 7 demonstra os volumes dos sortimentos determinados por integração da função de forma do tronco selecionada (equação 18), na qual são apresentados o dap, a altura total (h) com três valores para cada diâmetro, altura até o diâmetro de 25,0 cm com casca (h₂₅), a relação h/d (h/d), o volume até a altura com diâmetro com casca de 8,0 cm (v₈), o volume até a altura com diâmetro com casca de 25,0 cm (v₂₅), a percentagem do volume obtido até 25,0 cm de diâmetro em relação ao volume total (%), o volume da tora sem casca com diâmetro entre 8,0 e 25,0 cm (v_8-25) e os sortimentos (V25) para as classes S1, S2, S3, expressos em número de toras (n) e em percentagem do volume com casca, com diâmetro até 25,0 cm.

TABELA 7: Sortimentos para serraria de Eucalyptus grandis Hill ex Maiden.

TABLE 7: Sawmill assortments of Eucalyptus grandis Hill ex Maiden.

dap	h	h25	h/d	v8	v25		v8-25	SORTIMENTOS (V25)						PC
								S1		S2		S3
cm	m	m		m3 c/c	m3 c/c	%	m3 s/c	n	%	n	%	n	%	%
8,0	16,0	0,0	2,00	0,0075	0,0000	0,0	0,0064	0	0,0	0	0,0	0	0,0	14,7
8,0	16,8	0,0	2,10	0,0079	0,0000	0,0	0,0068	0	0,0	0	0,0	0	0,0	13,3
8,0	17,6	0,0	2,20	0,0083	0,0000	0,0	0,0072	0	0,0	0	0,0	0	0,0	12,2
9,0	17,2	0,0	1,92	0,0213	0,0000	0,0	0,0183	0	0,0	0	0,0	0	0,0	14,1
9,0	18,1	0,0	2,02	0,0224	0,0000	0,0	0,0196	0	0,0	0	0,0	0	0,0	12,9
9,0	19,0	0,0	2,12	0,0236	0,0000	0,0	0,0208	0	0,0	0	0,0	0	0,0	11,9
10,0	18,4	0,0	1,84	0,0395	0,0000	0,0	0,0341	0	0,0	0	0,0	0	0,0	13,6
10,0	19,4	0,0	1,94	0,0416	0,0000	0,0	0,0364	0	0,0	0	0,0	0	0,0	12,5
10,0	20,4	0,0	2,04	0,0438	0,0000	0,0	0,0387	0	0,0	0	0,0	0	0,0	11,6
11,0	19,6	0,0	1,78	0,0614	0,0000	0,0	0,0533	0	0,0	0	0,0	0	0,0	13,2
11,0	20,7	0,0	1,88	0,0649	0,0000	0,0	0,0569	0	0,0	0	0,0	0	0,0	12,2
11,0	21,8	0,0	1,98	0,0683	0,0000	0,0	0,0605	0	0,0	0	0,0	0	0,0	11,4
12,0	20,6	0,0	1,72	0,0863	0,0000	0,0	0,0752	0	0,0	0	0,0	0	0,0	12,9
12,0	21,8	0,0	1,82	0,0914	0,0000	0,0	0,0805	0	0,0	0	0,0	0	0,0	11,9
12,0	23,0	0,0	1,92	0,0964	0,0000	0,0	0,0856	0	0,0	0	0,0	0	0,0	11,2
13,0	21,6	0,0	1,66	0,1140	0,0000	0,0	0,0996	0	0,0	0	0,0	0	0,0	12,6
13,0	22,9	0,0	1,76	0,1208	0,0000	0,0	0,1067	0	0,0	0	0,0	0	0,0	11,7
13,0	24,2	0,0	1,86	0,1277	0,0000	0,0	0,1137	0	0,0	0	0,0	0	0,0	11,0
14,0	22,6	0,0	1,61	0,1444	0,0000	0,0	0,1266	0	0,0	0	0,0	0	0,0	12,3
14,0	24,0	0,0	1,71	0,1533	0,0000	0,0	0,1357	0	0,0	0	0,0	0	0,0	11,5
14,0	25,4	0,0	1,81	0,1623	0,0000	0,0	0,1447	0	0,0	0	0,0	0	0,0	10,8

TABELA 7: Continuação ...

TABLE 7: Continued …

dap	h	h25	h/d	v8	v25		v8-25	SORTIMENTOS (V25)						PC
								S1		S2		S3
cm	m	m		m3 c/c	m3 c/c	%	m3 s/c	n	%	n	%	n	%	%
15,0	23,5	0,0	1,57	0,1777	0,0000	0,0	0,1562	0	0,0	0	0,0	0	0,0	12,1
15,0	25,0	0,0	1,67	0,1890	0,0000	0,0	0,1677	0	0,0	0	0,0	0	0,0	11,3
15,0	26,5	0,0	1,77	0,2004	0,0000	0,0	0,1790	0	0,0	0	0,0	0	0,0	10,6
16,0	24,4	0,0	1,52	0,2141	0,0000	0,0	0,1887	0	0,0	0	0,0	0	0,0	11,8
16,0	26,0	0,0	1,62	0,2281	0,0000	0,0	0,2028	0	0,0	0	0,0	0	0,0	11,1
16,0	27,6	0,0	1,72	0,2422	0,0000	0,0	0,2168	0	0,0	0	0,0	0	0,0	10,5
17,0	25,2	0,0	1,48	0,2537	0,0000	0,0	0,2242	0	0,0	0	0,0	0	0,0	11,6
17,0	26,9	0,0	1,58	0,2709	0,0000	0,0	0,2413	0	0,0	0	0,0	0	0,0	10,9
17,0	28,6	0,0	1,68	0,2880	0,0000	0,0	0,2581	0	0,0	0	0,0	0	0,0	10,4
18,0	26,0	0,0	1,44	0,2968	0,0000	0,0	0,2627	0	0,0	0	0,0	0	0,0	11,5
18,0	27,8	0,0	1,54	0,3173	0,0000	0,0	0,2831	0	0,0	0	0,0	0	0,0	10,8
18,0	29,6	0,0	1,64	0,3379	0,0000	0,0	0,3033	0	0,0	0	0,0	0	0,0	10,2
19,0	26,7	0,0	1,41	0,3433	0,0000	0,0	0,3045	0	0,0	0	0,0	0	0,0	11,3
19,0	28,6	0,0	1,51	0,3677	0,0000	0,0	0,3286	0	0,0	0	0,0	0	0,0	10,6
19,0	30,5	0,0	1,61	0,3921	0,0000	0,0	0,3524	0	0,0	0	0,0	0	0,0	10,1
20,0	27,5	0,0	1,37	0,3934	0,0000	0,0	0,3495	0	0,0	0	0,0	0	0,0	11,1
20,0	29,5	0,0	1,47	0,4220	0,0000	0,0	0,3777	0	0,0	0	0,0	0	0,0	10,5
20,0	31,5	0,0	1,57	0,4507	0,0000	0,0	0,4055	0	0,0	0	0,0	0	0,0	10,0
21,0	28,1	0,0	1,34	0,4195	0,0000	0,0	0,3734	0	0,0	0	0,0	0	0,0	11,0
21,0	30,2	0,0	1,44	0,4508	0,0000	0,0	0,4040	0	0,0	0	0,0	0	0,0	10,4
21,0	32,3	0,0	1,54	0,4821	0,0000	0,0	0,4343	0	0,0	0	0,0	0	0,0	9,9
22,0	28,8	0,0	1,31	0,4733	0,0000	0,0	0,4219	0	0,0	0	0,0	0	0,0	10,9
22,0	31,0	0,0	1,41	0,5094	0,0000	0,0	0,4571	0	0,0	0	0,0	0	0,0	10,3
22,0	33,2	0,0	1,51	0,5455	0,0000	0,0	0,4919	0	0,0	0	0,0	0	0,0	9,8
23,0	29,5	0,0	1,28	0,5305	0,0000	0,0	0,4736	0	0,0	0	0,0	0	0,0	10,7
23,0	31,8	0,0	1,38	0,5720	0,0000	0,0	0,5138	0	0,0	0	0,0	0	0,0	10,2
23,0	34,1	0,0	1,48	0,6134	0,0000	0,0	0,5537	0	0,0	0	0,0	0	0,0	9,7
24,0	30,1	0,0	1,25	0,5913	0,0000	0,0	0,5286	0	0,0	0	0,0	0	0,0	10,6
24,0	32,5	0,0	1,35	0,6386	0,0000	0,0	0,5743	0	0,0	0	0,0	0	0,0	10,1
24,0	34,9	0,0	1,45	0,6857	0,0000	0,0	0,6196	0	0,0	0	0,0	0	0,0	9,6
25,0	30,7	1,8	1,23	0,6558	0,1056	16,1	0,4924	0	0,0	0	0,0	0	0,0	10,5
25,0	33,2	1,9	1,33	0,7092	0,1143	16,1	0,5357	0	0,0	0	0,0	0	0,0	10,0
25,0	35,7	2,1	1,43	0,7627	0,1229	16,1	0,5786	0	0,0	0	0,0	0	0,0	9,6
26,0	31,2	2,8	1,20	0,7238	0,1675	23,1	0,4986	0	0,0	0	0,0	1	98,8	10,4
26,0	33,8	3,1	1,30	0,7841	0,1815	23,1	0,5431	0	0,0	0	0,0	1	92,6	9,9
26,0	36,4	3,3	1,40	0,8443	0,1954	23,1	0,5873	0	0,0	0	0,0	1	87,1	9,5
27,0	31,8	4,0	1,18	0,7956	0,2372	29,8	0,5010	0	0,0	0	0,0	1	75,5	10,3
27,0	34,5	4,3	1,28	0,8631	0,2573	29,8	0,5465	0	0,0	1	97,8	0	0,0	9,8
27,0	37,2	4,7	1,38	0,9307	0,2775	29,8	0,5917	0	0,0	1	92,2	0	0,0	9,4
28,0	32,3	5,2	1,15	0,8711	0,3142	36,1	0,5002	0	0,0	1	84,9	0	0,0	10,2
28,0	35,1	5,6	1,25	0,9465	0,3414	36,1	0,5464	1	99,4	0	0,0	0	0,0	9,7
28,0	37,9	6,1	1,35	1,0220	0,3686	36,1	0,5923	1	93,8	0	0,0	0	0,0	9,3

TABELA 7: Continuação ...

TABLE 7: Continued …

dap	h	h25	h/d	v8	v25		v8-25	SORTIMENTOS (V25)						PC
								S1		S2		S3
cm	m	m		m3 c/c	m3 c/c	%	m3 s/c	n	%	n	%	n	%	%
29,0	32,8	6,4	1,13	0,9503	0,3984	41,9	0,4963	1	89,9	0	0,0	0	0,0	10,1
29,0	35,7	7,0	1,23	1,0343	0,4336	41,9	0,5430	1	84,3	0	0,0	0	0,0	9,6
29,0	38,6	7,6	1,33	1,1182	0,4687	41,9	0,5892	1	79,4	0	0,0	0	0,0	9,3
30,0	33,3	7,7	1,11	1,0333	0,4897	47,4	0,4893	1	78,6	0	0,0	0	0,0	10,0
30,0	36,3	8,4	1,21	1,1263	0,5338	47,4	0,5360	1	73,6	0	0,0	1	26,4	9,5
30,0	39,3	9,1	1,31	1,2193	0,5779	47,4	0,5824	1	69,2	0	0,0	1	24,9	9,2
31,0	33,8	7,6	1,09	1,0050	0,4812	47,9	0,4719	1	80,1	0	0,0	0	0,0	9,9
31,0	36,9	8,2	1,19	1,0972	0,5253	47,9	0,5177	1	75,0	0	0,0	0	0,0	9,5
31,0	40,0	8,9	1,29	1,1894	0,5695	47,9	0,5632	1	70,6	0	0,0	1	25,0	9,2
32,0	34,3	8,7	1,07	1,0865	0,5726	52,7	0,4634	1	72,0	0	0,0	1	25,2	9,8
32,0	37,5	9,6	1,17	1,1879	0,6260	52,7	0,5091	1	67,3	0	0,0	1	23,7	9,4
32,0	40,7	10,4	1,27	1,2894	0,6795	52,7	0,5545	1	63,3	1	32,7	0	0,0	9,1
33,0	34,7	9,9	1,05	1,1715	0,6697	57,2	0,4529	1	65,7	1	33,6	0	0,0	9,7
33,0	38,0	10,8	1,15	1,2828	0,7333	57,2	0,4982	1	61,3	1	31,5	0	0,0	9,3
33,0	41,3	11,8	1,25	1,3942	0,7970	57,2	0,5433	2	96,3	0	0,0	0	0,0	9,0
34,0	35,2	11,1	1,03	1,2600	0,7722	61,3	0,4406	1	60,6	1	31,0	0	0,0	9,7
34,0	38,6	12,1	1,13	1,3819	0,8468	61,3	0,4855	2	94,4	0	0,0	0	0,0	9,3
34,0	42,0	13,2	1,23	1,5036	0,9215	61,3	0,5298	2	88,8	0	0,0	0	0,0	9,0
35,0	35,6	12,2	1,02	1,3519	0,8796	65,1	0,4269	2	94,2	0	0,0	0	0,0	9,6
35,0	39,1	13,4	1,12	1,4850	0,9661	65,1	0,4711	2	88,0	0	0,0	0	0,0	9,2
35,0	42,6	14,6	1,22	1,6179	1,0527	65,1	0,5148	2	82,7	0	0,0	1	14,5	8,9
36,0	36,0	13,3	1,00	1,4475	0,9916	68,5	0,4124	2	88,7	0	0,0	0	0,0	9,5
36,0	39,6	14,6	1,10	1,5923	1,0908	68,5	0,4557	2	82,8	0	0,0	1	14,4	9,1
36,0	43,2	15,9	1,20	1,7371	1,1900	68,5	0,4985	2	77,7	1	20,0	0	0,0	8,9
37,0	36,4	14,3	0,98	1,5467	1,1077	71,6	0,3974	2	84,1	0	0,0	1	14,3	9,5
37,0	40,1	15,8	1,08	1,7039	1,2204	71,6	0,4397	2	78,4	1	19,9	0	0,0	9,1
37,0	43,8	17,2	1,18	1,8611	1,3330	71,6	0,4815	3	98,3	0	0,0	0	0,0	8,8
38,0	36,8	15,3	0,97	1,6492	1,2276	74,4	0,3821	2	80,3	0	0,0	1	13,7	9,4
38,0	40,6	16,9	1,07	1,8198	1,3544	74,4	0,4233	3	99,5	0	0,0	0	0,0	9,0
38,0	44,4	18,5	1,17	1,9901	1,4813	74,4	0,4641	3	93,7	0	0,0	0	0,0	8,8
39,0	37,1	16,3	0,95	1,7554	1,3508	77,0	0,3668	2	77,1	1	19,2	0	0,0	9,3
39,0	41,0	18,0	1,05	1,9399	1,4927	76,9	0,4071	3	95,5	0	0,0	0	0,0	9,0
39,0	44,9	19,8	1,15	2,1242	1,6346	76,9	0,4469	3	89,8	0	0,0	1	9,7	8,7
40,0	37,5	17,3	0,94	1,8651	1,4773	79,2	0,3519	3	98,3	0	0,0	0	0,0	9,3
40,0	41,5	19,1	1,04	2,0642	1,6349	79,2	0,3911	3	92,0	0	0,0	0	0,0	8,9
40,0	45,5	21,0	1,14	2,2632	1,7925	79,2	0,4298	3	86,5	0	0,0	1	9,4	8,7
41,0	37,8	18,2	0,92	1,9789	1,6068	81,2	0,3378	3	95,3	0	0,0	0	0,0	9,2
41,0	41,9	20,2	1,02	2,1931	1,7809	81,2	0,3757	3	89,1	0	0,0	1	9,2	8,9
41,0	46,0	22,1	1,12	2,4074	1,9549	81,2	0,4134	3	83,6	1	13,3	0	0,0	8,6
42,0	38,2	19,1	0,91	2,0956	1,7392	83,0	0,3238	3	92,7	0	0,0	0	0,0	9,2
42,0	42,4	21,2	1,01	2,3261	1,9305	83,0	0,3608	3	86,5	1	13,0	0	0,0	8,8
42,0	46,6	23,3	1,11	2,5567	2,1217	83,0	0,3976	4	97,8	0	0,0	0	0,0	8,6

TABELA 7: Continuação ...

TABLE 7: Continued …

dap	h	h25	h/d	v8	v25		v8-25	SORTIMENTOS (V25)						PC
								S1		S2		S3
cm	m	m		m3 c/c	m3 c/c	%	m3 s/c	n	%	n	%	n	%	%
43,0	38,5	19,9	0,90	2,2164	1,8744	84,6	0,3109	3	90,4	0	0,0	1	8,7	9,1
43,0	42,8	22,1	1,00	2,4637	2,0836	84,6	0,3468	3	84,3	1	12,8	0	0,0	8,8
43,0	47,1	24,4	1,10	2,7112	2,2929	84,6	0,3826	4	95,3	0	0,0	0	0,0	8,5
44,0	38,8	20,7	0,88	2,3407	2,0123	86,0	0,2986	3	88,4	0	0,0	1	8,6	9,0
44,0	43,2	23,1	0,98	2,6055	2,2403	86,0	0,3334	4	98,5	0	0,0	0	0,0	8,7
44,0	47,6	25,4	1,08	2,8709	2,4683	86,0	0,3684	4	93,1	0	0,0	1	6,4	8,5
45,0	39,1	21,5	0,87	2,4684	2,1531	87,2	0,2870	3	86,7	1	12,1	0	0,0	9,0
45,0	43,6	24,0	0,97	2,7520	2,4006	87,2	0,3210	4	96,5	0	0,0	0	0,0	8,7
45,0	48,1	26,4	1,07	3,0359	2,6480	87,2	0,3550	4	91,2	0	0,0	1	6,4	8,5
46,0	39,5	22,2	0,86	2,5999	2,2966	88,3	0,2762	3	85,2	1	12,0	0	0,0	8,9
46,0	44,1	24,8	0,96	2,9031	2,5644	88,3	0,3095	4	94,8	0	0,0	0	0,0	8,6
46,0	48,7	27,4	1,06	3,2061	2,8322	88,3	0,3425	4	89,5	1	9,0	0	0,0	8,4
47,0	39,7	23,0	0,85	2,7349	2,4429	89,3	0,2660	4	98,9	0	0,0	0	0,0	8,9
47,0	44,4	25,7	0,95	3,0584	2,7318	89,3	0,2986	4	93,3	0	0,0	1	5,9	8,6
47,0	49,1	28,4	1,05	3,3819	3,0207	89,3	0,3309	5	99,4	0	0,0	0	0,0	8,4
48,0	40,0	23,6	0,83	2,8738	2,5921	90,2	0,2568	4	97,5	0	0,0	0	0,0	8,8
48,0	44,8	26,5	0,93	3,2185	2,9029	90,2	0,2887	4	91,9	0	0,0	1	5,9	8,5
48,0	49,6	29,3	1,03	3,5629	3,2137	90,2	0,3200	5	97,9	0	0,0	0	0,0	8,3
49,0	40,3	24,3	0,82	3,0160	2,2742	91,0	0,2480	4	96,4	0	0,0	0	0,0	8,8
49,0	45,2	27,3	0,92	3,3828	3,0777	91,0	0,2792	4	90,7	1	8,3	0	0,0	8,5
49,0	50,1	30,2	1,02	3,7491	3,4113	91,0	0,3097	5	96,6	0	0,0	0	0,0	8,3
50,0	40,6	24,9	0,81	3,1622	2,8992	91,7	0,2400	4	95,3	0	0,0	0	0,0	8,7
50,0	45,6	28,0	0,91	3,5517	3,2564	91,7	0,2704	5	100,0	0	0,0	0	0,0	8,4
50,0	50,6	31,1	1,01	3,9412	3,6136	91,7	0,3005	5	95,4	0	0,0	1	4,2	8,3
51,0	40,8	25,5	0,80	3,3119	3,0571	92,3	0,2326	4	94,3	0	0,0	1	5,1	8,7
51,0	45,9	28,7	0,90	3,7253	3,4389	92,3	0,2624	5	99,0	0	0,0	0	0,0	8,4
51,0	51,0	31,9	1,00	4,1388	3,8206	92,3	0,2919	5	94,3	0	0,0	1	4,2	8,2
52,0	41,1	26,1	0,79	3,4652	3,2181	92,9	0,2257	4	93,4	0	0,0	1	5,2	8,6
52,0	46,3	29,4	0,89	3,9039	3,6253	92,9	0,2553	5	98,0	0	0,0	0	0,0	8,4
52,0	51,5	32,7	0,99	4,3419	4,0324	92,9	0,2840	5	93,3	1	6,0	0	0,0	8,2
53,0	41,3	26,7	0,78	3,6220	3,3822	93,4	0,2192	4	92,6	1	7,2	0	0,0	8,6
53,0	46,6	30,1	0,88	4,0863	3,8157	93,4	0,2481	5	97,2	0	0,0	0	0,0	8,3
53,0	51,9	33,5	0,98	4,5506	4,2493	93,4	0,2767	5	92,4	1	6,1	0	0,0	8,2
54,0	41,6	27,2	0,77	3,7822	3,5494	93,8	0,2129	4	91,9	1	7,3	0	0,0	8,6
54,0	47,0	30,8	0,87	4,2739	4,0102	93,8	0,2418	5	96,4	0	0,0	0	0,0	8,3
54,0	52,4	34,3	0,97	4,7647	4,4710	93,8	0,2698	6	99,3	0	0,0	0	0,0	8,1
55,0	41,8	27,7	0,76	3,9467	3,7197	94,2	0,2077	4	91,2	1	7,3	0	0,0	8,5
55,0	47,3	31,4	0,86	4,4660	4,2088	94,2	0,2360	5	95,7	0	0,0	1	3,7	8,2
55,0	52,8	35,0	0,96	4,9848	4,6979	94,2	0,2636	6	98,5	0	0,0	0	0,0	8,1
56,0	42,1	28,2	0,75	4,1147	3,8932	94,6	0,2028	5	99,7	0	0,0	0	0,0	8,5
56,0	47,7	32,0	0,85	4,6626	4,4115	94,6	0,2305	5	95,0	0	0,0	1	3,7	8,2
56,0	53,3	35,8	0,95	5,2102	4,9300	94,6	0,2576	6	97,8	0	0,0	0	0,0	8,1

 

TABELA 7: Continuação ...

TABLE 7: Continued …

dap	h	h25	h/d	v8	v25		v8-25	SORTIMENTOS (V25)						PC
								S1		S2		S3
cm	m	m		m3 c/c	m3 c/c	%	m3 s/c	n	%	n	%	n	%	%
57,0	42,3	28,7	0,74	4,2863	4,0699	95,0	0,1982	5	99,2	0	0,0	0	0,0	8,4
57,0	48,0	32,6	0,84	4,8643	4,6185	94,9	0,2257	5	94,4	1	5,3	0	0,0	8,2
57,0	53,7	36,5	0,94	5,4422	5,1672	94,9	0,2529	6	97,2	0	0,0	1	2,8	8,0
58,0	42,5	29,2	0,73	4,4611	4,2498	95,3	0,1936	5	98,7	0	0,0	0	0,0	8,4
58,0	48,3	33,2	0,83	5,0701	4,8298	95,3	0,2207	5	93,8	1	5,3	0	0,0	8,1
58,0	54,1	37,1	0,93	5,6786	5,4097	95,3	0,2473	6	96,5	0	0,0	1	2,8	8,0
59,0	42,7	29,6	0,72	4,6398	4,4329	95,5	0,1896	5	98,2	0	0,0	0	0,0	8,4
59,0	48,6	33,7	0,82	5,2807	5,0452	95,5	0,2164	6	99,9	0	0,0	0	0,0	8,1
59,0	54,5	37,8	0,92	5,9225	5,6578	95,5	0,2436	6	96,0	1	4,0	0	0,0	8,0
60,0	42,9	30,1	0,72	4,8222	4,6195	95,8	0,1858	5	97,8	0	0,0	0	0,0	8,3
60,0	48,9	34,3	0,82	5,4962	5,2653	95,8	0,2123	6	99,4	0	0,0	0	0,0	8,1
60,0	54,9	38,5	0,92	6,1708	5,9111	95,8	0,2391	6	95,4	1	4,1	0	0,0	8,0
61,0	43,1	30,5	0,71	5,0082	4,8092	96,0	0,1825	5	97,4	0	0,0	0	0,0	8,3
61,0	49,2	34,8	0,81	5,7166	5,4896	96,0	0,2088	6	99,0	0	0,0	0	0,0	8,0
61,0	55,3	39,1	0,91	6,4256	6,1701	96,0	0,2353	6	94,9	1	4,1	0	0,0	7,9
62,0	43,3	30,9	0,70	5,1979	5,0024	96,2	0,1794	5	97,0	0	0,0	1	3,0	8,2
62,0	49,5	35,3	0,80	5,9414	5,7184	96,2	0,2051	6	98,6	0	0,0	0	0,0	8,0
62,0	55,7	39,7	0,90	6,6857	6,4346	96,2	0,2313	7	99,6	0	0,0	0	0,0	7,9
63,0	43,5	31,3	0,69	5,3905	5,1988	96,4	0,1760	5	96,6	0	0,0	1	3,0	8,2
63,0	49,8	35,8	0,79	6,1712	5,9518	96,4	0,2019	6	98,2	0	0,0	0	0,0	8,0
63,0	56,1	40,3	0,89	6,9521	6,7046	96,4	0,2280	7	99,2	0	0,0	0	0,0	7,9
64,0	43,7	31,6	0,68	5,5873	5,3985	96,6	0,1734	5	96,3	0	0,0	1	3,0	8,2
64,0	50,1	36,3	0,78	6,4061	6,1894	96,6	0,1995	6	97,8	0	0,0	0	0,0	7,9
64,0	56,5	40,9	0,88	7,2242	6,9803	96,6	0,2248	7	98,8	0	0,0	0	0,0	7,8
65,0	43,9	32,0	0,67	5,7877	5,6016	96,8	0,1709	5	96,0	0	0,0	1	3,0	8,1
65,0	50,4	36,7	0,77	6,6452	6,4317	96,8	0,1966	6	97,5	0	0,0	1	2,3	7,9
65,0	56,9	41,5	0,87	7,5025	7,2617	96,8	0,2220	7	98,5	0	0,0	0	0,0	7,8
66,0	44,0	32,3	0,67	5,9913	5,8082	96,9	0,1683	5	95,7	1	4,2	0	0,0	8,1
66,0	50,6	37,2	0,77	6,8893	6,6784	96,9	0,1943	6	97,1	0	0,0	1	2,4	7,9
66,0	57,2	42,0	0,87	7,7868	7,5489	96,9	0,2193	7	98,1	0	0,0	1	1,9	7,8
67,0	44,2	32,7	0,66	6,1982	6,0180	97,1	0,1657	5	95,4	1	4,3	0	0,0	8,1
67,0	50,9	37,6	0,76	7,1381	6,9300	97,1	0,1918	6	96,8	0	0,0	1	2,4	7,9
67,0	57,6	42,6	0,86	8,0777	7,8420	97,1	0,2175	7	97,8	0	0,0	1	1,9	7,8
68,0	44,4	33,0	0,65	6,4096	6,2313	97,2	0,1639	5	95,1	1	4,3	0	0,0	8,0
68,0	51,2	38,0	0,75	7,3919	7,1861	97,2	0,1897	6	96,5	1	3,4	0	0,0	7,8
68,0	58,0	43,1	0,85	8,3737	8,1408	97,2	0,2148	7	97,4	0	0,0	1	1,9	7,7
69,0	44,5	33,3	0,65	6,6239	6,4480	97,3	0,1618	5	94,8	1	4,4	0	0,0	8,0
69,0	51,4	38,5	0,75	7,6505	7,4470	97,3	0,1876	6	96,2	1	3,4	0	0,0	7,8
69,0	58,3	43,6	0,85	8,6768	8,4458	97,3	0,2131	7	97,1	1	2,8	0	0,0	7,7
70,0	44,7	33,6	0,64	6,8428	6,6679	97,4	0,1609	6	100,0	0	0,0	0	0,0	8,0
70,0	51,7	38,9	0,74	7,9138	7,7123	97,5	0,1858	6	95,9	1	3,5	0	0,0	7,8
70,0	58,7	44,1	0,84	8,9853	8,7565	97,5	0,2112	7	96,8	1	2,8	0	0,0	7,7

TABELA 7: Continuação ...

TABLE 7: Continued …

dap	h	h25	h/d	v8	v25		v8-25	SORTIMENTOS (V25)						PC
								S1		S2		S3
cm	m	m		m3 c/c	m3 c/c	%	m3 s/c	n	%	n	%	n	%	%
71,0	44,9	33,9	0,63	7,0643	6,8917	97,6	0,1589	6	99,8	0	0,0	0	0,0	7,9
71,0	52,0	39,3	0,73	8,1824	7,9826	97,6	0,1843	7	100,0	0	0,0	0	0,0	7,7
71,0	59,1	44,6	0,83	9,3004	9,0734	97,6	0,2096	7	96,5	1	2,9	0	0,0	7,7
72,0	45,0	34,2	0,63	7,2889	7,1184	97,7	0,1570	6	99,6	0	0,0	0	0,0	7,9
72,0	52,2	39,6	0,73	8,4550	8,2572	97,7	0,1826	7	99,8	0	0,0	0	0,0	7,7
72,0	59,4	45,1	0,83	9,6215	9,3960	97,7	0,2082	8	99,8	0	0,0	0	0,0	7,6
73,0	45,2	34,5	0,62	7,5173	7,3488	97,8	0,1552	6	99,4	0	0,0	0	0,0	7,9
73,0	52,5	40,0	0,72	8,7331	8,5368	97,8	0,1812	7	99,5	0	0,0	0	0,0	7,7
73,0	59,8	45,6	0,82	9,9482	9,7247	97,8	0,2065	8	99,6	0	0,0	0	0,0	7,6
74,0	45,3	34,7	0,61	7,7491	7,5820	97,8	0,1540	6	99,3	0	0,0	0	0,0	7,9
74,0	52,7	40,4	0,71	9,0152	8,8210	97,8	0,1793	7	99,3	0	0,0	0	0,0	7,7
74,0	60,1	46,1	0,81	10,2821	10,0597	97,8	0,2055	8	99,4	0	0,0	0	0,0	7,6

Em que: dap = diâmetro à altura do peito (1,30 m), em centímetros; h = altura total da árvore, com três valores para cada diâmetro, em metros; h₂₅ = altura até o diâmetro de 25,0 cm casca, em metros; h/d = relação h/d; v₈ = volume até a altura com diâmetro com casca de 8,0 cm, em metros cúbicos; v₂₅ = volume até a altura com diâmetro com casca de 25,0 cm, em  metros  cúbicos;  % = percentagem  do  volume  obtido  até   25,0  cm  de  diâmetro  em  relação ao volume total; v_8-25 = volume da tora sem casca com diâmetro entre 8,0 e 25,0 cm, em metros cúbicos; S1, S2 e S3 = classes de sortimentos; n = número de toras; % = percentagem do volume com casca, com diâmetro até 25,0 cm; PC = percentagem de casca.

CONCLUSÕES

Os resultados obtidos no presente trabalho permitiram concluir que:

a) O polinômio do quinto grau foi, entre as equações de forma testadas, o que apresentou melhor precisão estatística e permitiu estimar com segurança o número de toras e o volume relativo dos sortimentos de madeira da espécie.

b) Os volumes e sortimentos relativos das classes de sortimento podem ser utilizados com segurança em inventários florestais da espécie para classes diamétricas entre 8,0 cm e 74,0 cm, tanto para estimar volume como para os sortimentos de madeira, pois os resíduos do volume real com o estimado pela equação polinomial do quinto grau foram pequenos.

c) O procedimento adotado para a determinação dos sortimentos das classes, previamente definidas, permitiu obter estimativas do número de toras e seus volumes relativos com boa precisão.

REFERÊNCIAS BIBLIOGRÁFICAS

• JOKELA, P.R. Die Schaftformfunktion der Fichte und die Bestimung der Sortmentsanteile am Stehenden Stam. 1974. Tese (Doutorado) – Zurich, Diss. D. ETH.
• KOZAK, A.;  MUNRO, D.D.; SMITH, J.H.G. Taper Function and their Aplications in Forest Inventory. For. Chron., v. 45, n. 4, p. 278-283, 1969.
• LEMOS, R.C.; AZOLIN, M.A.D.; ABRÃO, P.V.R. ; SANTOS, N.C.L. Levantamento de reconhecimento dos solos do Estado do Rio Grande do Sul. Recife: Ministério da Agricultura, Departamento de Pesquisas Agropecuárias - Divisão de Pesquisas de Pesquisas Pedológicas, 1973. 431p. (Boletim Técnico, 30).
• MORENO, J.A. Clima do Rio Grande do Sul. Porto Alegre: Secretaria da Agricultura-RS., 1961. 41p.
• PRODAN, M. Holzmesslehre. Frankfurt : J. D. Suaerlander’s , 1965. 643p.
• SCHNEIDER, P.R. Betriebswirtschaftliche und Ertragskundliche Grundlagen der Forsteinrichtung in Südbrasilien am Beispiel von Pinus elliottii. 1984. 190p. Tese (Tese de Doutorado) ­–  Albert-Ludwigs-Universität, Freiburg, 1984
• SCHNEIDER, P.R. Introdução ao manejo florestal. Santa Maria: UFSM /CEPEF/ FATEC, 1998. 348p.
• SPURR, S.H. Forest Inventory. New York: The Ronald Press, 1952. 476p.
• SAS. Statistical analysis system: programa de computador, ambiente VM. Cary, 1993. Versão 6.08.

Copyright 2005 - Ciência Florestal