Journal of Applied Sciences and Environmental Management World Bank assisted National Agricultural Research Project (NARP) - University of Port Harcourt ISSN: 1119-8362 Vol. 11, Num. 4, 2007, pp. 147-149

Journal of Applied Sciences and Environmental Management, Vol. 11, No. 4, 2007, pp. 147-149

Exact Solutions for Chebyshev Equations by using the Asymptotic Iteration Method

SOUS A. J. *, M. AL-HAWARI¹

Department of Mathematics, Al-Quds Open University, Nablus Email: melhem_fan@hotmail.com
¹Department of Mathematics, Al-jouf University, Askaka, Saudi Arabia

* Corresponding author: Sous A. J

Code Number: ja07112.

ABSTRACT:

The asymptotic iteration method is used in order to solve the Chebyshev differential equations, and to reproduce the Chebyshev polynomials of the first and second kinds respectively. It is shown that the asymptotic iteration method is valid for any degree .

The Chebyshev polynomials are important in many areas of mathematics, and physics. Particularly in the approximation theory since the roots of the Chebyshev polynomials of the first kind are used in the polynomial interpolation [1]. In the study of differential equations, Chebyshev polynomials arise as the solution to the Chebyshev differential equations

(1-x²) yn''(x) -x yn'(x) +n² y_n(x) =0, (1)

and

[[(1-x²) yn''(x)-3x yn'(x)+n(n+2) yn(x)=0,]] (2)

where n = 0 , 1, 2 , 3 , ... for the polynomials T_n (x), U_n (x) of the first and second kinds respectively [2,8]. These equations are special case of the Sturm-Liouville equation [3].

Chebyshev polynomials are used virtually in the field of numerical analysis, and it holds particular importance in different subjects including orthogonal polynomials, and polynomial approximation. Ell-gendi [4] has extensively shown how Chebyshev polynomials can be used to solve linear integral equations, integro-differential equations, and ordinary differential equations. Various methods for solving linear and nonlinear ordinary differential equations [5, 6, 7] were devised at about the same time and were based on the discrete orthogonality relationships of the Chebyshev polynomials.

In the literature [2, 8], the Chebyshev differential equations has been solved very heavily using the power series solution method. The reader may face several problems in following the power series solution technique, in which guessing the solution in many cases is very difficult task. Therefore, we applied a new method, the asymptotic iteration method (AIM) [9] to solve this kind of differential equations, where we don’t need to use the recurrence relation to find the general solution. This method is very easy to implement in the case of Chebyshev differential equations. The results of this method are very accurate. Moreover, the reader can obtain the solutions without a strong background in mathematics. The paper is organized as follows: in section 2 we will describe the AIM to solve the Chebyshev differential equations. In section 3 our analytical results for the Chebyshev polynomials, and then we conclude and remark therein.

2. Formalism of the asymptotic iteration method for the Chebyshev differential equations

The starting point to apply the AIM is to rewrite equations (1) and (2) in the following form:

yn '' (x)= k₀ (x) y_n (x) + z₀ (x) y_n (x) (3)

Where k₀ (x) and z₀ (x) are defined for equations (1), and (2) as:

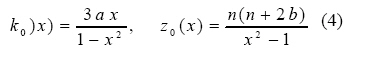
Note that for equation equation (2)a = b = 1.

In order to find a general solution to equation (3) we rely on the symmetric structure of the right -hand side of equation (3). Thus if we differentiate equation (3) with respect to , we obtain [9-12]

y"n ( x)= k₁ (x) y_n (x) + z₁ (x) y_n (x) (5)

where

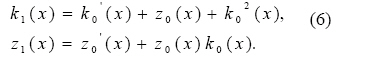
Likewise, the calculations of the second derivative of equation (3) yield

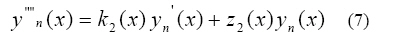
where

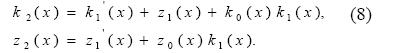
Thus for (j+1) and (j+2)^th

derivatives, j = 1, 2, 3, ..we have

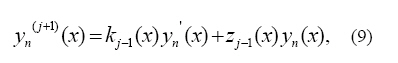
and

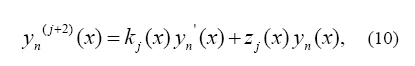
respectively, where

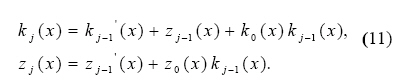
The ratio of the ( j + 1 ) and ( j + 2 ) th derivatives can be expressed as

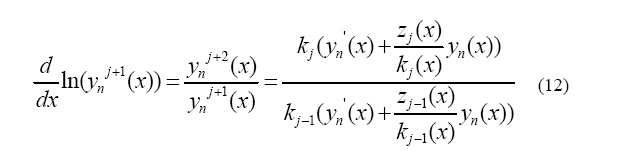
For sufficiently large j , we can introduce the”asymptotic” aspect of the method, that is

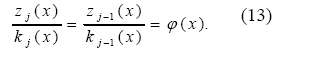
Thus equation (12) can be reduced to

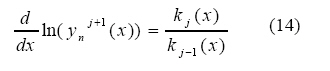
which yields

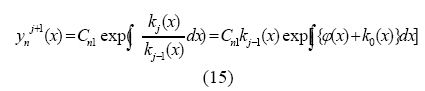
Where C_n1 is the integration constant, and the right-hand of equation (15) follows from equation (11), and the definition of φ (x) . Substituting equation (15) into equation (9) we obtain a first-order differential equation

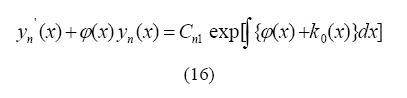
This, in turn, yields the general solution to the equation (3)

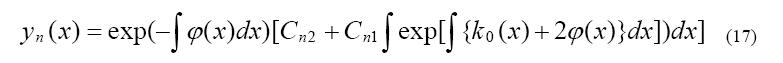
Maple software producing a constant of the form

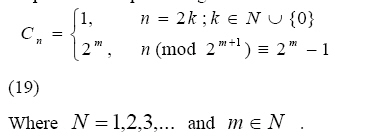
The results of our calculations with different values of n are given, so that the reader may, if so inclined reproduce our results.

Case (1): The first few Chebyshev polynomials of the first kind are

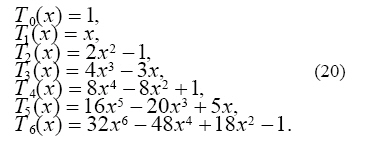
Case (2): The first few Chebyshev polynomials of the second kind are

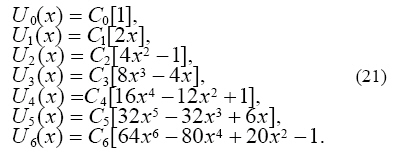
In all cases, we have only considered the sixth order of polynomials of the first and second kinds. This was so to make a clear comparison between the results of this method and the results of [2, 8]. The obtained polynomials are all in excellent agreement with the exact ones.

REFERENCES

• Johan P. Boud, November 2003. Chebyshev polynomial expansions for simultaneous approximation of two branches of a function with application to the one dimensional Bratu equation. Applied Mathematics and Computation, Volume 143, Issuses 2-3, 189-200.
• Wikipedia, November 2002. Chebyshev polynomials. The free encyclopedia, Versio 1.2.
• Heli Chen, and Bernie D. Shizgal, 2001. A spectral solution of the SturmLiouville equation, Journal of Computational and Applied Mathematics, 136 17-35.
• El-gendi S E, 1969. Comput. J (U K)12 282.
• Streltsov I. P, 2000. J. Computer Physics Communications. 126 178-181.
• Ayegul Akyu-Daciolu, 2004. J. Applied Mathematics and Computation. 151 221-232.
• V. J Ervin, and E. P. Stephan 1992. Journal of Computational and Applied Mathematics. 43 221-229.
• Handbook of Differential Equations, 1997, 3rd ed. Boston, MA: Academic Press.
• H. Ciftci, Hall R L, and, Saad N, 2003. J. phys. A : Math. Gen. 36 11807.
• A. J. Sous, J. Mod. Phys. Lett. A, 21, 1675 (2006).
• A. J. Sous, Chin. J. Phys. 44, 167 (2006).
• A. J. Sous, J. Mod. Phys. Lett. A, 22, 1677 (2007).

Copyright 2007 - Journal of Applied Sciences & Environmental Management